Exploring ECDSA (Elliptic Curve Digital Signature Algorithm)
In the realm of cryptography, security and authenticity are paramount. Digital signatures play a pivotal role in ensuring data integrity and verifying the identity of the sender. One of the most widely used digital signature algorithms is the Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA offers a robust and efficient way to sign and verify digital messages, making it a cornerstone of modern secure communication systems. In this article, we will delve into the workings of ECDSA, its mathematical underpinnings, its strengths, and its applications.
The Need for Digital Signatures
In today's interconnected world, digital communication is ubiquitous. However, this convenience comes with a price – the risk of unauthorized access, tampering, and forgery. Digital signatures are a cryptographic technique that addresses these concerns by providing authentication and data integrity. A digital signature allows the recipient of a message to verify its origin and ensure that it hasn't been altered during transmission.
Understanding ECDSA
ECDSA, the Elliptic Curve Digital Signature Algorithm, is a cryptographic technique that employs elliptic curve cryptography (ECC) to create and verify digital signatures. ECC is based on the mathematical properties of elliptic curves, which offer a unique blend of strong security and computational efficiency.
Mathematical Foundations of ECDSA
At the heart of ECDSA lies the mathematical concept of elliptic curves. An elliptic curve is a smooth curve defined by an equation of the form: *y² = x³ + ax + b*, where *a* and *b* are constants. The curve also contains a point at infinity, denoted as *O*, which serves as the identity element for addition on the curve.
ECDSA utilizes the discrete logarithm problem on elliptic curves to provide its security. In simple terms, finding the discrete logarithm involves determining the value *k* for a given point *P* such that *kP* equals a known point *Q*. This problem is computationally difficult, forming the basis for the security of ECC-based algorithms like ECDSA.
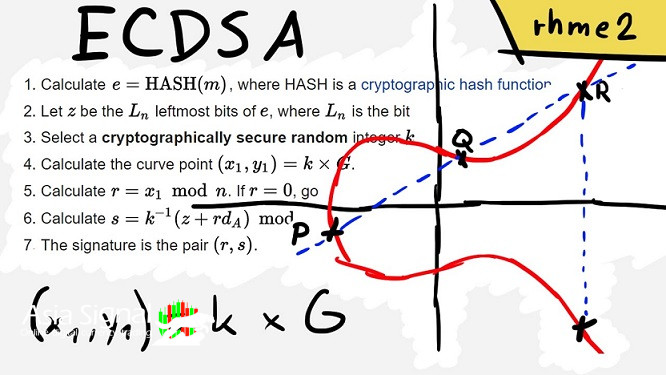
Key Generation
ECDSA operates with a pair of cryptographic keys: a private key and a corresponding public key. The private key is a randomly generated secret number, while the public key is derived from the private key using elliptic curve operations.
1. Private Key Generation: A random number *d* is chosen as the private key, where *1 < d < n - 1*, and *n* is the order of the elliptic curve's base point.
2. Public Key Derivation: The public key is calculated as *Q = dG*, where *G* is the base point of the elliptic curve, and *Q* is the resulting public key.
Signing and Verifying with ECDSA
Signing Process:
1. Message Hashing: The message to be signed is first hashed using a cryptographic hash function, usually SHA-256.
2. Creating the Signature: To sign the message hash, the signer performs the following steps:
- Generates a random value *k*, where *1 < k < n - 1*.
- Computes the point *P = kG*.
- Calculates the x-coordinate of *P* modulo *n* and denoted as *r*.
- Computes the modular inverse of *k* modulo *n* and denoted as *k⁻¹*.
- Calculates the signature parameter *s* using the formula *s = k⁻¹ * (hash + dr)*, where *hash* is the message hash and *d* is the signer's private key.
3. Sending the Signature: The signer sends the pair (*r*, *s*) as the digital signature along with the original message.
Verification Process:
1. Message Hashing: The received message is hashed using the same cryptographic hash function to obtain the message hash.
2. Signature Verification: The verifier performs the following steps:
- Checks if *r* and *s* are within the range [1, n - 1].
- Computes the value of *w* as the modular inverse of *s* modulo *n*.
- Calculates two points on the curve: *u1 = hash * w* and *u2 = r * w*.
- Calculates the point *V = u1G + u2Q*, where *Q* is the public key of the signer.
- If the x-coordinate of *V* modulo *n* equals *r*, the signature is valid; otherwise, it is invalid.
Benefits and Applications of ECDSA
ECDSA offers several advantages that make it a popular choice for digital signatures:
1. Security-Performance Trade-off: ECDSA provides strong security with shorter key lengths compared to traditional RSA, resulting in faster computations and less memory usage.
2. Compact Signatures: ECDSA signatures are relatively small, making them ideal for resource-constrained environments like IoT devices.
3. Efficient Verifications: Verifying ECDSA signatures is computationally efficient, making it suitable for high-throughput applications like financial transactions.
4. Blockchain Technology: ECDSA is extensively used in blockchain networks to ensure the authenticity of transactions and the security of digital assets.
5. Digital Identity: ECDSA is employed in digital identity systems to verify users' identities and protect their sensitive information.
Challenges and Considerations
While ECDSA offers numerous benefits, there are also challenges and considerations to keep in mind:
1. Parameter Selection: Proper selection of elliptic curve parameters is crucial for security. Inadequate choices can lead to vulnerabilities.
2. Random Number Generation: Secure random number generation is vital for the algorithm's security. Flawed random number generators can lead to predictable signatures.
3. Side-Channel Attacks: Side-channel attacks, such as timing attacks and power analysis, can compromise the security of the implementation if not properly mitigated.

Conclusion
In the digital age, securing data and verifying authenticity are paramount concerns. The Elliptic Curve Digital Signature Algorithm (ECDSA) has emerged as a robust solution to these challenges, offering a potent blend of security and efficiency. By leveraging the mathematical properties of elliptic curves, ECDSA provides a solid foundation for digital signatures, ensuring that messages are untampered and sent by legitimate parties. With applications ranging from blockchain technology to digital identity systems, ECDSA continues to play a pivotal role in shaping the secure communication landscape. Understanding its mathematical foundations, benefits, challenges, and considerations is crucial for anyone involved in cryptography and secure communication systems.
you can find best Crypto signal leaks in Asiasignal

















Comments